Factoring Quadratics With Python

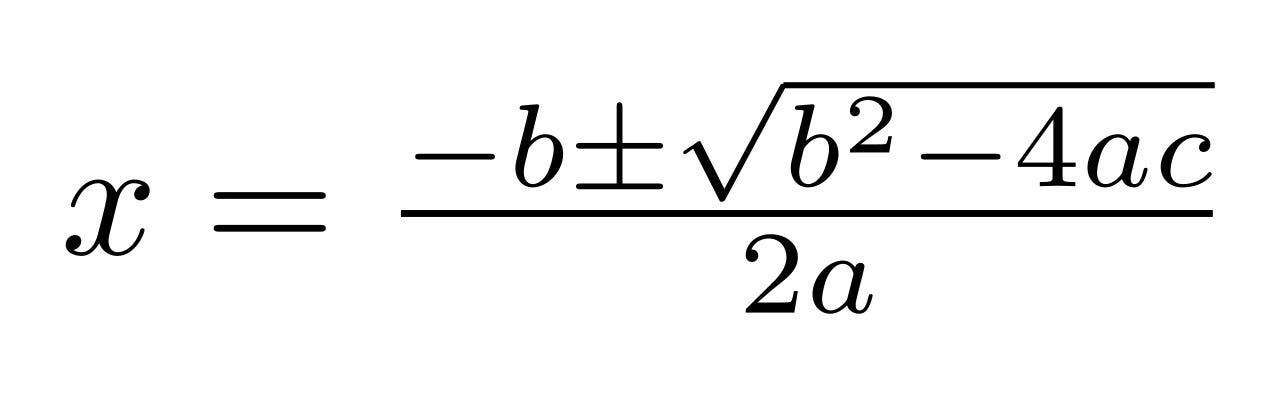
We are going to write a Python program that takes a quadratic of the form $ax^2+bx+c$ and puts it into factored form $a(bx+c)(dx+e)$. Our program will only factor problems where the roots are integers or rational fractions (e.g., $\frac{3}{4}$).

We will start off by making our program take the three variables as inputs and converting the inputs to float numbers.

Now we are going to perform the first step of factoring: finding the greatest common divisor (GCD) between our three terms. We will be writing our own GCD function. Our function will, in essence, swap the two numbers, making the new first number $a$ equal to $b$ and the new $b$ equal to $b \bmod a$. It will keep doing this until $b$ is zero.

Since our function can only take the GCD of two numbers at a time, we will call our gcdCalc function twice: once with the first two numbers, and once again with the previous result and the last number.

Now that we have found the GCD, we are capable of factoring quadratics of the simplest form—ones where the constant $c$ is equal to zero. All we have to do is factor out the GCD and an $x$ term and output the result.

Our code up until this point should look like the following:

We can now factor any quadratic where the constant is zero:

But we want to be able to factor all sorts of quadratics. So we are going to add an else statement to our c==0 statement we wrote above, and we are going to start off by finding the two possible solutions using the quadratic equation.

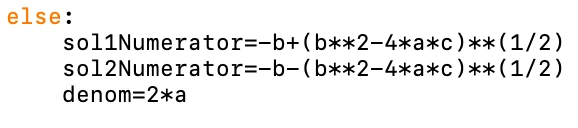
Note: Both solutions in the quadratic equation have the same denominator, which I have calculated separately.

We are now going to check if any of our three values are non-integer. If so, we know that we won’t have a “clean” factorization of all integers, so we want to abort the factorization process.

Our last step will be to find the GCD between our numerator and denominator so that we can reduce our fractions.

We now want to generate the numerators and denominators of our solution. Note that we will be taking the negative of the numerator because the quadratic formula gives us the roots $x=x_1$ or $x=x_2$, but we want to put it in the form $x-x_1=0$ or $x-x_2=0$, so we will be taking the negative of our numerators.

We will now print out our factored quadratic:

Note that we are multiplying the GCD by $\frac{a}{|a|}$ to ensure that we get the same sign as $a$.

Our finished code now looks like the following:

We can now test it out:

We can also try out some other quadratics:

But the $\pm$ kind of bothers me, so I’m going to write a function that will display the correct sign:

Now I’m going to modify my two print statements to make use of my function:

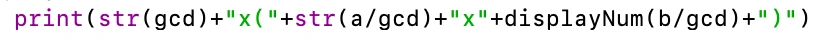
Now our outputs look like the following:

Here’s a copy of the code we have written together:

def displayNum(x):
    if x>0:
        return " + "+str(x)
    elif x==0:
        return ""
    else:
        return " - "+str(abs(x))

print("please enter your variable values assuming the form ax^2+bx+c")
a=float(input("a: "))
b=float(input("b: "))
c=float(input("c: "))

def gcdCalc(a,b):
    while b:
        temp=a
        a = b
        b=temp%b
    return abs(a)

gcdTemp=gcdCalc(a,b)
gcd=gcdCalc(gcdTemp,c)

if c==0:
    print(str(gcd)+"x("+str(a/gcd)+"x"+displayNum(b/gcd)+")")
else:
    sol1Numerator=-b+(b**2-4*a*c)**(1/2)
    sol2Numerator=-b-(b**2-4*a*c)**(1/2)
    denom=2*a
    if not (sol1Numerator.is_integer() and sol2Numerator.is_integer()) or not denom.is_integer():
        print("no clean factorization")
    else:
        sol1Gcd=gcdCalc(sol1Numerator,denom)
        sol2Gcd=gcdCalc(sol2Numerator,denom)
        sol1Numerator=-sol1Numerator/sol1Gcd
        sol1Denominator=denom/sol1Gcd
        sol2Numerator=-sol2Numerator/sol2Gcd
        sol2Denominator=denom/sol2Gcd
        print(str(gcd*a/abs(a))+"("+str(sol1Denominator)+"x"+displayNum(sol1Numerator)+")("+str(sol2Denominator)+"x"+displayNum(sol2Numerator)+")")