Finding a Function's Roots with Python

Python is a versatile programming language, but finding function roots (solving for $f(x) = 0$) without libraries like SciPy can be complex. Symbolic algebraic solving—isolating $x$—is difficult to implement due to the vast array of mathematical operations and identities (e.g., trigonometric substitutions). Consequently, numerical methods are often preferred for their generality.

In this tutorial, we will implement the Newton-Raphson method to find roots numerically. While libraries like SciPy offer robust solutions, building a solver from scratch provides valuable insight into numerical analysis.

The Newton-Raphson Method

The Newton-Raphson method is an iterative algorithm that approximates roots using tangent lines. The process is as follows:

1. Initial Guess: Start with an estimate $x_0$ for the root.
2. Evaluate: Check if $f(x_0)$ is close to zero. If so, we have found a root.
3. Tangent Line: Calculate the tangent line of the function at $x_0$.
4. Update: Find where the tangent line intersects the x-axis. Let this intersection be the new guess, $x_1$.
5. Repeat: Iterate this process until a solution is found or the maximum number of iterations is reached.

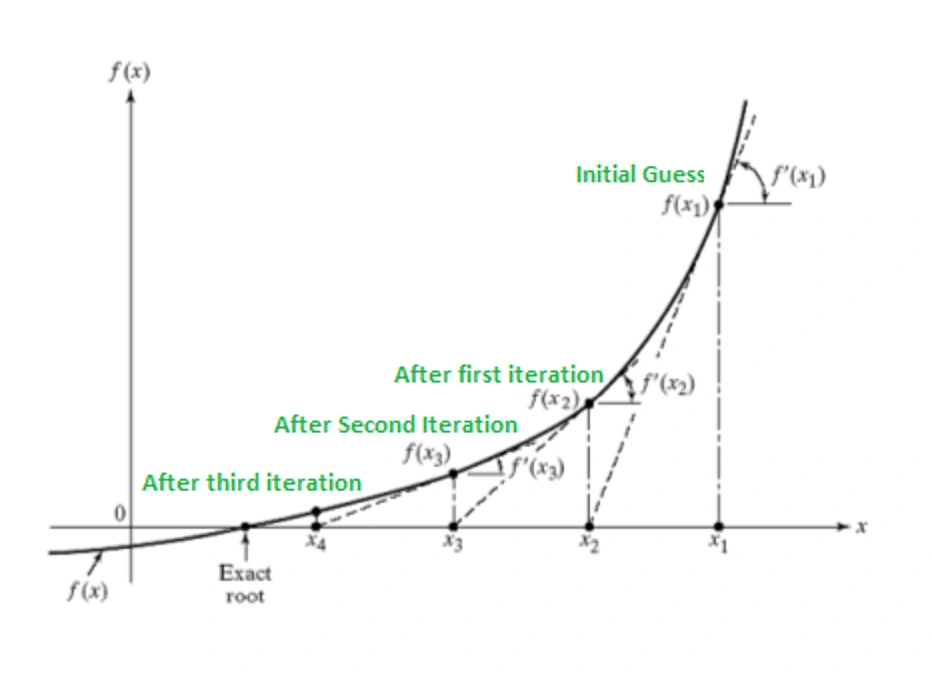
Note that this method is not guaranteed to converge and may produce false positives. It typically finds one root per initial guess, so we will need to sweep over a domain to find multiple roots.

Implementation

We will define a function solver that performs the Newton-Raphson algorithm.

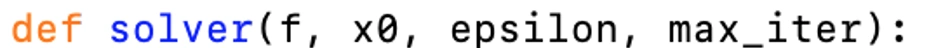
First, we initialize xn to our starting guess x0 and begin a loop that runs up to max_iter times:

Inside the loop, we calculate y = f(xn). If its absolute value is within epsilon of zero, we return xn as the solution.

If not, we calculate the slope of the tangent line. We approximate the derivative using the difference quotient $f'(x) \approx \frac{f(x+h)-f(x)}{h}$ with a small $h$.

Using the point-slope form, the x-intercept of the tangent line provides our next guess:

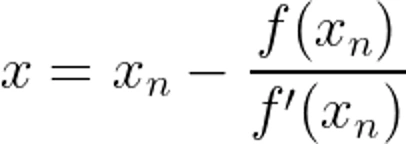
Translating this to code:

We must handle the edge case where the slope is zero (horizontal tangent), which would cause a division by zero. In this case, we return None. Finally, if the loop finishes without converging, we return None.

Testing the Solver

Let’s test the function with an example:

By varying x0, we can find different roots. Lowering epsilon increases precision:

This implementation mirrors the logic used by many scientific calculators, which also require an initial guess.

Scientific calculators like the Casio fx-991EX often use the Newton-Raphson method under the hood for their equation solvers. Just like our Python script, they require an initial guess (often defaulting to zero if not provided) and iterate until they find a solution within a certain tolerance!

Finding Multiple Roots

To find all roots within a range, we can create a loop function that sweeps through the domain $[L\_bound, R\_bound]$ with a specified increment, calling solver at each step.

Inside the loop, we call solver:

We round valid solutions to avoid duplicates (e.g., treating 0.00001 and -0.00001 as distinct roots) and store unique results in a list.

Finally, we print the sorted solutions.

Execution

Note that the solver may converge to roots outside the initial search domain, as the domain only dictates the initial guesses.

Handling Singularities

To prevent crashes at undefined points (like $x=0$ in $1/x$), we wrap the function evaluation in a try-except block.

If a ZeroDivisionError occurs, we return a small number to allow the algorithm to continue, though this is a heuristic approach.

Limitations

1. False Positives: The solver may incorrectly identify a root near an asymptote where the function approaches zero but never touches it (e.g., $1/x$).
2. Performance: The algorithm may be slow for functions with no roots.
3. Discontinuities: While it can handle some discontinuities, roots may be missed if they lie between increments or near jumps.
4. Domain: We only scan a finite domain; roots outside this range (that aren’t reached by the basin of attraction of our guesses) will be missed.

This method can also solve for intersections of two functions, say $g(x)$ and $h(x)$, by finding the roots of $f(x) = g(x) - h(x)$.

Complete Code

def derivative(f, x):
    h = 1e-8
    return (f(x+h)-f(x))/h

def solver(f, x0, epsilon, max_iter):
    xn = x0
    for n in range(0, max_iter):
        y = f(xn)
        if abs(y) < epsilon:
            return xn
        slope = derivative(f, xn)
        if slope == 0:
            return None
        xn = xn - y/slope
    return None

def loop(f, L_bound, R_bound, increment):
    solutions = []
    while L_bound <= R_bound:
        solution = solver(f, L_bound, 1e-10, 1000)
        if solution is not None:
            solution = round(solution, 4)
            if solution not in solutions:
                solutions.append(solution)
        L_bound += increment
    print(sorted(solutions))
    print("we found " + str(len(solutions)) + " solutions!")

equation = ""

def f(x):
    try:
        y = eval(equation)
    except ZeroDivisionError:
        y = 1e-10
    return y

equation = "x**2-9"
loop(f, -100, 100, 0.5)