Finding odd roots of negative numbers with python

If you’ve ever tried to take the odd root of a negative number such as:

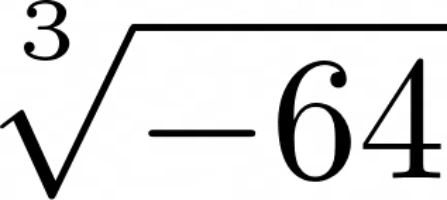
With a generic calculator such as the Casio fx-991EX, you’d see that the third root of negative 64 is negative 4. However, if you plug that same equation into the Python shell, you will see the following:

This may seem confusing at first, but it is a complex number of the form a+bj where a=2 and b=3.46410 (note that Python displays complex numbers using ‘j’ instead of ‘i’). By the fundamental theorem of algebra, we know that every real number has n nth roots. You can read about the fundamental theorem of algebra here . If you plug our equation into an online calculator such as Wolfram Alpha , you will see that the three solutions for our question are as follows:

If you compare these solutions to the one that Python outputs, you will see that Python gave us the root that is referred to by Wolfram as the “principal root”. The principal root is the root of the form a+bi where a and b are both non-negative (in this case a=2 and b=3.4631).

Python will always return the principal root when taking any root of any number.

Our Solution:

If we remember middle school algebra, we know that the nth root of x is just a number that, when multiplied by itself n times, gives us x.

When x is less than zero we can rewrite the problem as follows:

Since n is odd we can then move the negative sign out from under the root:

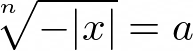
Since taking the nth root of a positive number always gives us a real number in Python, we have effectively derived an equation that will find the real solution to an odd root of a negative number:

We can turn our idea into a Python function. We want to start off by checking if the root we are trying to find is negative. If not, we can just return the root found the normal way; otherwise, we want to use the equation we created above:

Now, to find the third root of negative 64, we can just call our function:

This function will find any root of any number as long as a real solution exists. If a real solution does not exist, the function will return numbers that are completely wrong.

A real solution will never exist if you are trying to take the even root of a negative number, that is, when n%2=0 and f<0.