Finding Vertical Asymptotes with Python

This tutorial builds upon the concepts introduced in my previous article on Finding a Function’s Roots with Python . It is recommended to review that article first, as we will reuse the root-finding algorithm implemented there.

Understanding Vertical Asymptotes

Vertical asymptotes are vertical lines $x = c$ that the graph of a function approaches as $x$ tends to $c$. For rational functions (functions expressed as a ratio of two polynomials $\frac{P(x)}{Q(x)}$), vertical asymptotes typically occur where the denominator is zero, provided the numerator is non-zero at that point.

If both the numerator and denominator are zero at a certain point, this usually indicates a “hole” (removable discontinuity) rather than a vertical asymptote.

For a more detailed explanation, you can read my post on What are Vertical Asymptotes? .

Implementation Strategy

Our program will find vertical asymptotes for rational functions by following these steps:

1. Accept the numerator and denominator as separate inputs from the user.
2. Find the roots (zeros) of the denominator.
3. Evaluate the numerator at these roots.
4. If the numerator is non-zero, the root corresponds to a vertical asymptote.

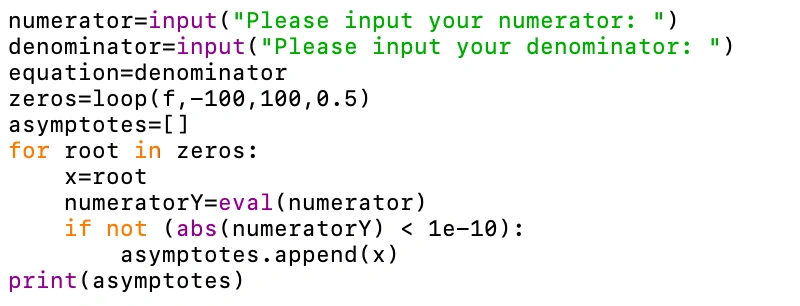
1. User Input

We start by accepting the numerator and denominator as strings.

2. Reusing the Root Solver

We will adapt the solver and loop functions from the previous root-finding tutorial. We modify the loop function to return a list of solutions instead of printing them directly.

3. Finding Candidates

We find the zeros of the denominator using our root solver. These are the candidate values for vertical asymptotes.

4. Verifying Asymptotes

We iterate through the found roots (zeros) and evaluate the numerator at each point.

Here, we use Python’s built-in eval function to dynamically evaluate the user’s mathematical expression. Note that eval should be used with caution in production environments due to security risks, but it is acceptable for this local script.

If the value of the numerator at a root is not close to zero (i.e., abs(numeratorY) >= 1e-10), we identify it as a vertical asymptote. If it is close to zero, it indicates a removable discontinuity (a hole).

Finally, we print the identified asymptotes.

Testing the Program

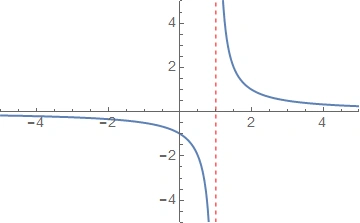
Let’s test the program with the function $\tan(x) = \frac{\sin(x)}{\cos(x)}$.

The program correctly identifies the vertical asymptotes of $\tan(x)$ over the finite domain.

Now, let’s consider a rational function with a hole: $\frac{x-3}{x^2-9}$. Since $x^2-9 = (x-3)(x+3)$, the term $(x-3)$ cancels out, leaving a hole at $x=3$ and a vertical asymptote at $x=-3$.

Our program correctly filters out $x=3$ and identifies only $x=-3$ as the vertical asymptote.

Complete Code

The full implementation, including the Newton-Raphson solver, is provided below:

import math

def derivative(f, x):
    h = 1e-8
    return (f(x+h)-f(x))/h

def solver(f, x0, epsilon, max_iter):
    xn = x0
    for n in range(0, max_iter):
        y = f(xn)
        if abs(y) < epsilon:
            return xn
        slope = derivative(f, xn)
        if slope == 0:
            return None
        xn = xn - y/slope
    return None

def loop(f, L_bound, R_bound, increment):
    solutions = []
    while L_bound <= R_bound:
        solution = solver(f, L_bound, 1e-10, 1000)
        if solution is not None:
            solution = round(solution, 4)
            if solution not in solutions:
                solutions.append(solution)
        L_bound += increment
    return sorted(solutions)

equation = ""

def f(x):
    try:
        y = eval(equation)
    except ZeroDivisionError:
        y = 1e-10
    return y

numerator = input("Please input your numerator: ")
denominator = input("Please input your denominator: ")
equation = denominator
zeros = loop(f, -100, 100, 0.5)
asymptotes = []

for root in zeros:
    x = root
    numeratorY = eval(numerator)
    if not (abs(numeratorY) < 1e-10):
        asymptotes.append(x)
print(asymptotes)