Fixing SymPy's Limit Calculator Flaw

SymPy is a Python library written entirely in python that aims to become a full-featured computer algebra system (CAS) while keeping its code as simple as possible.

If you ever have to do advanced mathematical operations with Python, I’d highly recommend SymPy. It’s capable of solving equations, plotting graphs, taking integrals and most other mathematical operations you can think of. However, like any tool, SymPy has its limitations. In this post, we’ll explore a significant flaw in SymPy’s limit calculator when dealing with functions that have limited domains or jump discontinuities, and we’ll implement a solution to fix it.

A limit is the value that a function approaches as the input (x value) approaches some value. More precisely, it’s the value that the function gets arbitrarily close to as the input gets arbitrarily close to the target point. For example, the limit of x/x as x approaches zero would be written as follows:

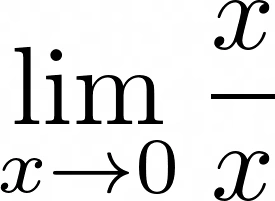
The format of SymPy’s limit function is as follows

sympy.limit(function, variable, point, direction)

For this particular limit our function call would look as follows:

sympy.limit(x/x, x, 0)

We did not include the optional direction parameter because our limit approaches from both directions (SymPy’s default)

Our function graphed looks as follows:

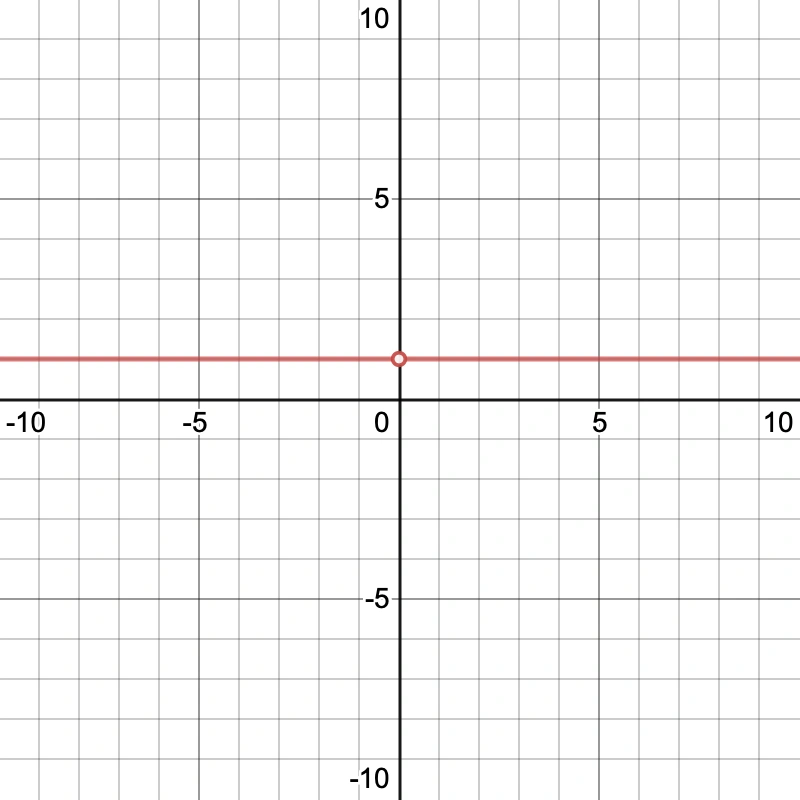
Although our function is not defined at x=0 because dividing by zero is indeterminate, it does appear that our function approaches 1 as x approaches zero, so SymPy does appear correct in this instance.

However, SymPy’s limit calculator has some significant flaws that become apparent when dealing with more complex functions. Let’s explore these issues.

The Problem

If we take a function that has a limited domain (a function that is only defined for certain input values) such as the square root of x and we try to find the limit as our function approaches zero from the left, SymPy gives us the following result:

But if we look at the graph I’ve attached below, sqrt(x) has a domain from [0,+∞), so it is literally impossible to approach from the left.

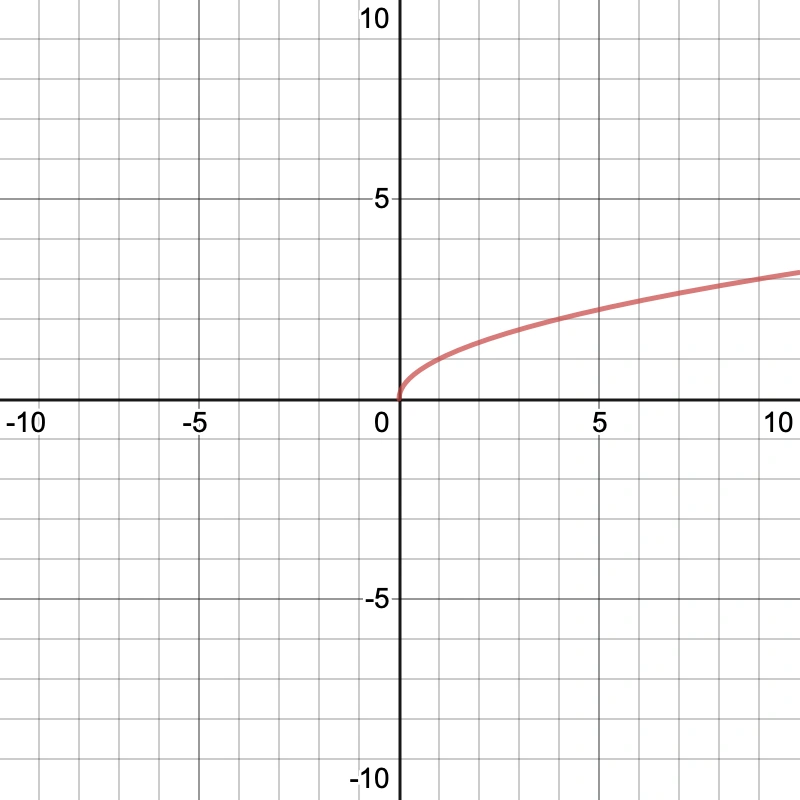
SymPy doesn’t respect the functions domain when calculating limits

Another case where SymPy will give us incorrect results is if we take a function like x/|x| (which represents the sign function) that I’ve graphed below and try to take its limit as x approaches zero.

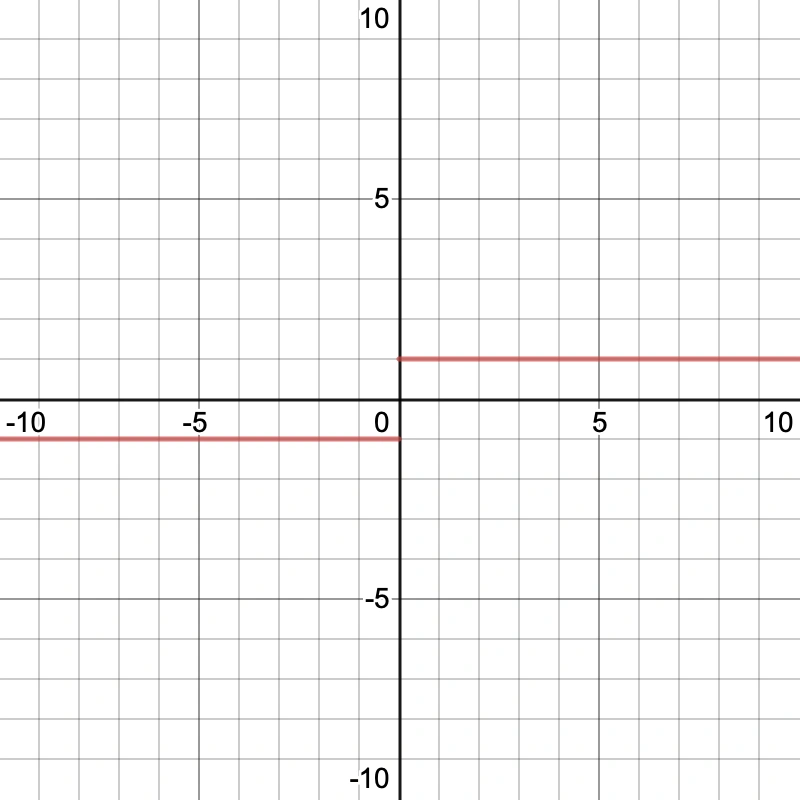
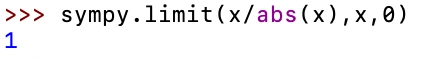
This result is obviously incorrect as our function approaches a different value from the left than it does from the right. If we take the one-sided limits with SymPy we get:

These limits are correct. Since the two one-sided limits are different, the two-sided limit does not exist.

SymPy struggles to take limits of any function containing jump discontinuities

Why This Happens

This occurs because of the way SymPy calculates limits. SymPy uses series expansion to approximate the function’s value at the desired point. Here’s a video by PatrickJMT solving a limit using series expansion. This method works well for “well-behaved” functions—those that are continuous and smooth in the neighborhood around the point of interest. However, it’s inherently flawed when dealing with functions that have jump discontinuities or domain restrictions. Since series expansion is just an approximation, the location of any jump discontinuity may be shifted ever so slightly in either direction. This method also fails to take into account any domain issues our limit may face.

Now that we understand why these problems occur, let’s implement a solution that addresses these limitations.

The Solution

Our approach is conceptually similar to the epsilon-delta definition of a limit , which states that if a limit exists, the closer we get to our point from either side (horizontally), the smaller the range of our function on that interval becomes. As our domain becomes smaller (centered around the x value we are approaching), the range of our function using that domain will eventually become so small that it approaches a single number—which is what we call our limit.

Our solution will be to approximate the limit by calculating a point on the appropriate side(s) of our desired limit that is incredibly close to the value we are approaching to see if the limit exists. This approach directly checks the function’s behavior near the point of interest, rather than relying on series expansion.

We will start off by differentiating between our 3 cases: left limit, right limit, and normal (bi-directional) limit.

def fixed_limit(function, variable, point, approachFrom=None):
    """
    Calculate the limit of a function at a given point, with improved handling
    for functions with limited domains or jump discontinuities.
    
    Parameters:
    - function: The SymPy expression representing the function
    - variable: The variable to take the limit with respect to
    - point: The point at which to evaluate the limit
    - approachFrom: Direction to approach from ('-' for left, '+' for right, None for both)
    
    Returns:
    - The limit value if it exists, or an error string if it doesn't
    """
    if approachFrom == '-':
        pass
    elif approachFrom == '+':
        pass
    else:
        pass

The “pass” statements are just there as placeholders for code

If it’s a limit from the left, we are going to test if our function is defined at a number slightly smaller than the one we are approaching. I will use 1e-8 to the left of our number (1e-8 is incredibly small—it represents one divided by one hundred million, or 1/100,000,000). The choice of 1e-8 is a balance between being close enough to detect domain issues while avoiding numerical precision problems. To verify that our function is defined to the left of our desired point, we want to check if that number is real. If so, we will run the SymPy function; if not, we will return an error message.

if approachFrom == '-':
    # Test point slightly to the left (1e-8 units away)
    testPoint = point - 1e-8
    testValue = function.subs(variable, testPoint)
    if testValue.is_real:
        return sympy.limit(function, variable, point, approachFrom)
    else:
        return "Error: function is not defined to the left of this point"

Based on our knowledge of limits, the first one should be an error and the second should be a number close to zero.

Seems as if we are doing okay so far. Now we will expand this concept to right-sided limits by adding our very small number (1e-8) to the number we are approaching to obtain a point that’s to the right of our limit.

elif approachFrom == '+':
    # Test point slightly to the right (1e-8 units away)
    testPoint = point + 1e-8
    testValue = function.subs(variable, testPoint)
    if testValue.is_real:
        return sympy.limit(function, variable, point, approachFrom)
    else:
        return "Error: function is not defined to the right of this point"

Now for our final situation, the two-sided limit: we will calculate both one-sided limits and check if they’re both valid (not error strings) and equal. If both limits exist and are close enough, we will assume that the limit exists and run SymPy; otherwise, we will return an error.

else:
    leftLimit = fixed_limit(function, variable, point, '-')
    rightLimit = fixed_limit(function, variable, point, '+')
    # Check if either limit returned an error (string) or if they differ significantly
    if isinstance(leftLimit, str) or isinstance(rightLimit, str):
        return "Error: limit does not exist, one or both one-sided limits are undefined"
    elif abs(leftLimit - rightLimit) < 1e-10:
        return sympy.limit(function, variable, point)
    else:
        return "Error: limit does not exist, the two one-sided limits are different"

Note how we don’t include approachFrom in our else statement as a parameter for sympy.limit because the two-sided limit is the default behavior.

We can now test our code with some of the problems we found above:

Complete Code

Here’s the complete implementation:

import sympy

def fixed_limit(function, variable, point, approachFrom=None):
    """
    Calculate the limit of a function at a given point, with improved handling
    for functions with limited domains or jump discontinuities.
    
    Parameters:
    - function: The SymPy expression representing the function
    - variable: The variable to take the limit with respect to
    - point: The point at which to evaluate the limit
    - approachFrom: Direction to approach from ('-' for left, '+' for right, None for both)
    
    Returns:
    - The limit value if it exists, or an error string if it doesn't
    """
    if approachFrom == '-':
        # Test point slightly to the left (1e-8 units away)
        # This threshold balances closeness with numerical precision
        testPoint = point - 1e-8
        testValue = function.subs(variable, testPoint)
        if testValue.is_real:
            return sympy.limit(function, variable, point, approachFrom)
        else:
            return "Error: function is not defined to the left of this point"
    elif approachFrom == '+':
        # Test point slightly to the right (1e-8 units away)
        testPoint = point + 1e-8
        testValue = function.subs(variable, testPoint)
        if testValue.is_real:
            return sympy.limit(function, variable, point, approachFrom)
        else:
            return "Error: function is not defined to the right of this point"
    else:
        # Two-sided limit: check both one-sided limits
        leftLimit = fixed_limit(function, variable, point, '-')
        rightLimit = fixed_limit(function, variable, point, '+')
        # Check if either limit returned an error (string) or if they differ significantly
        # The threshold 1e-10 accounts for floating-point precision differences
        if isinstance(leftLimit, str) or isinstance(rightLimit, str):
            return "Error: limit does not exist, one or both one-sided limits are undefined"
        elif abs(leftLimit - rightLimit) < 1e-10:
            return sympy.limit(function, variable, point)
        else:
            return "Error: limit does not exist, the two one-sided limits are different"

Conclusion

We’ve successfully implemented a solution that addresses SymPy’s limitations when calculating limits for functions with restricted domains or jump discontinuities. Our fixed_limit function respects function domains by checking if functions are defined at test points, handles jump discontinuities by comparing one-sided limits, and provides clear error messages when limits don’t exist. This solution is particularly useful when working with functions that have limited domains (like square roots or logarithms), dealing with functions containing absolute values or other piecewise components, or when SymPy’s default limit calculator returns unexpected results.

While this solution improves upon SymPy’s default behavior, it’s worth noting that the thresholds (1e-8 for test points, 1e-10 for limit comparison) are somewhat arbitrary and may need adjustment for extreme cases. The function also still relies on SymPy’s underlying limit calculation once domain checks pass, inheriting any other SymPy limitations. This approach demonstrates how understanding mathematical foundations (like the epsilon-delta definition) can guide us to practical solutions for computational problems.