The Power Rule for Derivatives

The power rule is used to find the derivative of polynomial terms. It tells us that the derivative of $x^n$ will be $nx^{n-1}$ for any real n.

Visualization

The easiest way to visualize this is to use it to take the derivative of $x^2$. We can let n=2 and use the rule we learned above to find the derivative to be $2x$.

You can verify your solution by randomly drawing tangents on $x^2$ and seeing how the slope of those tangents will always be equal to $2x$. Take x=0 as an example: the slope of our tangent at zero would be zero (a horizontal line) and 2(0)=0.

This is shown on our graph below where the red line is our original function, the blue line is our derivative, and the green line is our tangent at zero.

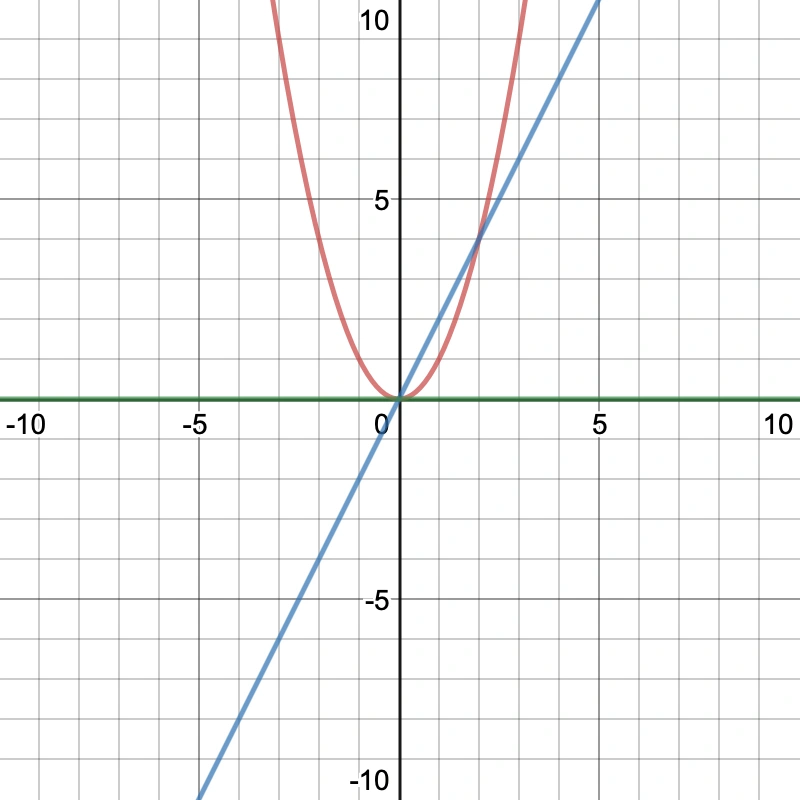
Notation

The derivative is commonly indicated with either a “prime”/“apostrophe” (’) or with Leibniz notation we can write: $\frac{d}{dx}$, which means the same thing.

So if $f(x) = x^n$ is our original, we could write the derivative as $f'(x) = nx^{n-1}$ or as: $\frac{d}{dx} f(x) = nx^{n-1}$.

Derivative of $\sqrt{x}$

We can rewrite $\sqrt{x}$ as $x^{\frac{1}{2}}$. We can then apply our power rule by letting $n = \frac{1}{2}$:

We can now conclude that:

Memorization Trick

All you need to remember to do is to multiply by the power, then subtract 1 from the power (reduce the power by 1).

A Table of Examples

These examples are completely random and have been chosen to help you memorize the power rule:

Pro Tips

• Works with any real number, not just integers
• Multiply n by the coefficient of x, then subtract 1 from the power
• The derivative will always be an order 1 less than the original
• The derivative at a local min or max will always be zero as the tangent will be horizontal

THANKS FOR READING